In the ever-evolving world of computer science, algorithms serve as the backbone of almost all computer-based tasks. Whether it’s processing data, performing calculations, or automating tasks, algorithms are essential in shaping how computers solve problems. Understanding algorithms is crucial for every programmer, from novice to expert, because they directly impact the efficiency, scalability, and performance of your code.
Key Takeaways:
- Efficiency Matters: Understanding the time and space complexity of algorithms helps you choose the best solution for your problem.
- Problem-Specific Algorithms: Different problems require different algorithms—mastering a wide range allows you to adapt to any challenge.
- Practice is Key: Implement these algorithms in code regularly to understand their behavior and nuances.
- Understand Trade-Offs: Every algorithm comes with its own set of trade-offs. Choose one that fits the problem context.
- Real-World Applications: Many of these algorithms are used in daily software applications like GPS navigation, data analytics, and game development.
Introduction to Algorithms
An algorithm is a step-by-step procedure or formula for solving a problem. It serves as the blueprint for writing computer programs that process data and generate outputs based on certain inputs. Algorithms are the key to efficient and optimized coding.
When you start learning algorithms, it’s important to grasp the basic concepts such as time complexity, space complexity, and how different algorithms compare when solving a problem. The algorithm’s efficiency can make the difference between a program that runs instantly and one that lags or fails.
Below, we’ll explore the top 10 essential algorithms every programmer should understand and implement. Mastering these algorithms will give you a solid foundation for tackling a wide variety of programming challenges.
Sorting Algorithms
Sorting algorithms are crucial for organizing data efficiently. They play a significant role in searching, data processing, and optimizing the use of resources.
- Quick Sort: A divide-and-conquer algorithm that divides the array into sub-arrays, sorts them independently, and then merges them. It’s highly efficient with an average-case time complexity of O(n log n).
- Merge Sort: Another divide-and-conquer algorithm with a time complexity of O(n log n). It divides the list into two halves, sorts them recursively, and merges them.
- Bubble Sort: While not the most efficient, bubble sort is a simple sorting algorithm that repeatedly compares and swaps adjacent elements. Its time complexity is O(n²) in the worst case.
- Insertion Sort: An efficient algorithm for small datasets, where the array is sorted by repeatedly taking an element from the unsorted part and inserting it into its correct position. Its worst-case time complexity is O(n²).
Why It Matters: Sorting is a fundamental operation. Whether you’re working with databases, performing analytics, or developing applications, understanding sorting algorithms is crucial for optimizing data processing.
Binary Search
The binary search algorithm is a fast way to search for a specific element in a sorted array.
- Process: The algorithm works by repeatedly dividing the search interval in half. If the target value is less than the middle value, the search continues on the left half, and if it’s greater, the search continues on the right half.
- Time Complexity: O(log n), which makes it highly efficient for searching compared to linear search (O(n)).
Why It Matters: Binary search is essential for optimizing search operations in large datasets. Mastering binary search can significantly improve the speed of your algorithms.
Dijkstra’s Algorithm
Dijkstra’s algorithm is used for finding the shortest path between nodes in a graph. It works with graphs that have non-negative edge weights.
- Process: The algorithm starts at a given node and explores all neighboring nodes, calculating the cumulative distance. It then selects the node with the smallest tentative distance and proceeds until the shortest path to the destination node is found.
- Time Complexity: O(V²) with a simple implementation, but with optimized data structures like a priority queue, the time complexity reduces to O((V + E) log V).
Why It Matters: Dijkstra’s algorithm is used in routing and navigation systems, such as GPS, network routing protocols, and flight planning systems. It’s crucial for problems involving optimization and graph traversal.
Depth-First Search (DFS) and Breadth-First Search (BFS)
Both DFS and BFS are graph traversal algorithms that are essential for exploring graphs and solving problems like pathfinding and cycle detection.
- DFS: DFS explores as deep as possible along each branch before backtracking. It uses a stack (or recursion) to keep track of the nodes.
- BFS: BFS explores all nodes at the present depth level before moving on to nodes at the next depth level. It uses a queue to track nodes.
- Time Complexity: Both DFS and BFS have a time complexity of O(V + E), where V is the number of vertices and E is the number of edges.
Why It Matters: These algorithms are essential in scenarios like web crawling, shortest path finding, and social network analysis. BFS is often used for unweighted shortest path problems, while DFS is useful for tasks like solving puzzles and mazes.
Knapsack Problem (Dynamic Programming)

The Knapsack problem is a classical optimization problem often solved using dynamic programming (DP). The goal is to maximize the value of items placed in a knapsack, subject to a weight constraint.
- Problem: Given a set of items, each with a weight and a value, determine the maximum value that can be achieved with a knapsack of limited capacity.
- Time Complexity: O(nW), where n is the number of items and W is the weight capacity of the knapsack.
Why It Matters: The Knapsack problem and its solutions are crucial in resource allocation problems, such as budget management, cargo loading, and project scheduling.
Floyd-Warshall Algorithm
The Floyd-Warshall algorithm is an all-pairs shortest path algorithm used to find the shortest paths between all pairs of nodes in a weighted graph.
- Process: The algorithm systematically checks all pairs of nodes and iterates over all potential intermediate nodes to find the shortest possible path.
- Time Complexity: O(V³), where V is the number of vertices.
Why It Matters: This algorithm is used in network routing protocols and in applications that require finding shortest paths between multiple points.
Heap Sort
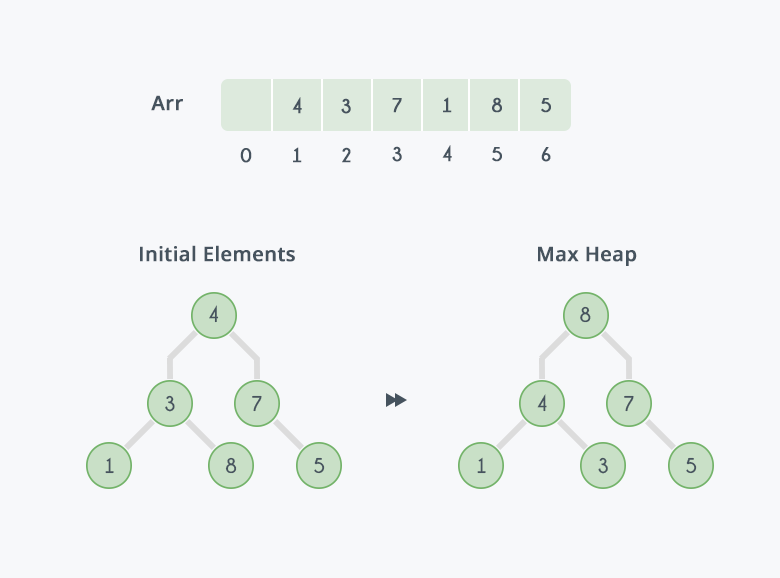
Heap sort is a comparison-based sorting algorithm that uses a binary heap data structure to sort elements.
- Process: The algorithm first builds a heap from the input data, then repeatedly extracts the maximum element from the heap and rebuilds the heap until the list is sorted.
- Time Complexity: O(n log n) for both average and worst-case scenarios.
Why It Matters: Heap sort is efficient and can be used in applications that require sorting large datasets, as it has better worst-case time complexity than algorithms like quicksort or bubble sort.
A Search Algorithm*
The A search algorithm* is widely used in pathfinding and graph traversal. It’s an extension of Dijkstra’s algorithm that adds a heuristic to estimate the distance to the goal.
- Process: A* combines the advantages of both DFS and BFS by considering the current cost to reach a node and a heuristic estimate of the remaining distance to the goal.
- Time Complexity: The time complexity varies, but it is generally O(E), where E is the number of edges, depending on the graph structure and heuristic used.
Why It Matters: A* is used in applications such as GPS navigation, robotics, and video games to find the most efficient path.
Merge Intervals
The merge intervals algorithm is commonly used to solve problems that involve overlapping intervals, such as meeting room scheduling.
- Process: The algorithm sorts the intervals by start time, then iterates through them and merges overlapping intervals into a single interval.
- Time Complexity: O(n log n) due to the sorting step.
Why It Matters: This algorithm is useful in scheduling, resource allocation, and time management applications.
Topological Sorting
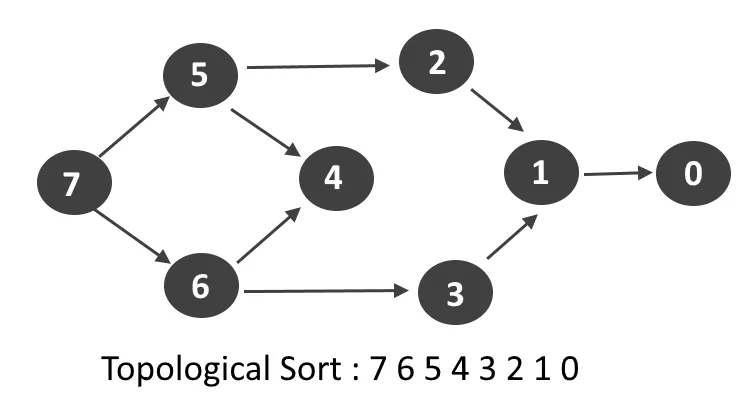
Topological sorting is used to order elements in a Directed Acyclic Graph (DAG). It is crucial for problems like task scheduling and dependency resolution.
- Process: The algorithm arranges vertices such that for every directed edge uv, vertex u comes before v in the ordering.
- Time Complexity: O(V + E), where V is the number of vertices and E is the number of edges.
Why It Matters: Topological sorting is essential for scheduling tasks in a project, building dependency graphs in compilers, and resolving package dependencies.
Also Read : Mca Placement: Opportunities, Top Companies, And Tips For Success
Conclusion
Mastering algorithms is a fundamental part of becoming a proficient programmer. These 10 essential algorithms represent key problem-solving techniques used in various real-world applications. Whether you’re sorting data, finding the shortest path, or optimizing your code, these algorithms are building blocks you’ll often rely on.
Frequently Asked Questions (FAQs)
What is the difference between sorting algorithms like Merge Sort and Quick Sort?
Merge Sort is stable and guarantees O(n log n) time complexity, while Quick Sort is faster in practice but has O(n²) worst-case performance.
Which algorithm should I use for searching a large dataset?
If the dataset is sorted, Binary Search is the optimal choice due to its O(log n) time complexity.
How do I choose between DFS and BFS?
Use DFS when the solution requires exploring deep paths or if memory usage is a concern, and BFS for finding the shortest path in unweighted graphs.
What are some real-world applications of the A search algorithm?*
A* is used in GPS navigation, video games, and robotics for efficient pathfinding and navigation.
When should I use Dynamic Programming?
Use Dynamic Programming for problems that have overlapping subproblems and optimal substructure, such as the Knapsack Problem or Fibonacci sequence.
What is a graph traversal algorithm?
DFS and BFS are common graph traversal algorithms used to explore nodes in a graph.
What is the advantage of the Floyd-Warshall algorithm over Dijkstra’s?
Floyd-Warshall is better when you need to find the shortest path between all pairs of nodes, while Dijkstra’s is used for finding the shortest path from a single source.







